Quiz 3 - Sections 1.4-1.5

(1) Where are the following functions not continuous? Are the discontinuities removable? What are the vertical asymptotes (if any)?

(a)

$$f(x)= \frac{x-4}{x^2-6x+8}$$

Solving for the denominator, we get x²-6x+8=(x-4)(x-2), so the discontinuities are at the points x=2 and x=4. When we find the limit $\lim_{x \to 2} \frac{x-4}{x^2-6x+8}$ we get an undefined limit (unbounded behavior), and thus 2 is a non-removable discontinuity. On the other hand, $\lim_{x \to 4} \frac{x-4}{x^2-6x+8}= \frac{1}{2}$, so if we re-defined $f(4)=\frac{1}{2}$, then f would be continuous at the point x=4, and at 4 there is a removable discontinuity. x=2 is the vertical asymptote of f(x). This can be seen from a graph, and also from the fact that there is unbounded behavior at x=2 (checking limits).

(b)

$$g(x)= \left\{ \begin{array}{ll} \frac{x+2}{2} & x \leq 2 \\ \frac{-x}{x-3} & x > 2 \\ \end{array} \right.$$

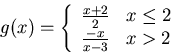
For a piecewise function you should check the points in between the pieces for continuity. But since $\lim_{x \to 2^-} \frac{x+2}{2} = 2$ and $\lim_{x \to 2^+} \frac{-x}{x-3} = 2$, the function is continuous at x=2. Now you should also check the function pieces. $\frac{x+2}{2}$ is continous everywhere (in particular, for $x \leq 2$), while $\frac{-x}{x-3}$ has a discontinuity at x=3. This discontinuity is non-removable, and there is an asymptote at x=3.

(2) (True or False) If $\lim_{x \to c} f(x) = L$ and f(c)=L, then f is continuous at c.

This is true. A function is continuous at a point, c, when both $\lim_{x \to c} f(x) = L$ and f(c)=L.

(3) Find the following limit:

$$\lim_{x \to 3^{+}} \frac{x-2}{x-3}.$$

I accepted the answer ``undefined'', but the answer $\infty$ is the best answer. $\lim_{x \to 3^{+}} \frac{x-2}{x-3} = \infty$ says more than that the limit is undefined.