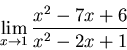
Exam 1 Practice - Limits and Derivatives
Part I
(1) Calculate the following limits:
(a)
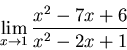
First try direct substitution, but
![]() .
Therefore we have to try something else, and considering that we have
two rational functions, it seems that factoring might be the way to go.
SO
.
Therefore we have to try something else, and considering that we have
two rational functions, it seems that factoring might be the way to go.
SO
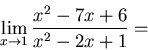

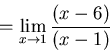
(b)
Again try direct substitution first: again the result is
![]() ,
so we have to do something else. This looks quite similar to the limit
we saw in class:
,
so we have to do something else. This looks quite similar to the limit
we saw in class:
![]() .
We must use this
limit:
.
We must use this
limit:
(c)
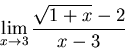
For the third straight time try direct substitution, and again we get
![]() .
Now this one has square root in it, so factoring doesn't
look good nor can we compare to a known limit. Here looks like a perfect
time to use rationalization:
.
Now this one has square root in it, so factoring doesn't
look good nor can we compare to a known limit. Here looks like a perfect
time to use rationalization:
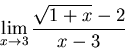
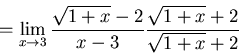
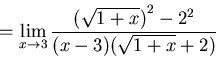
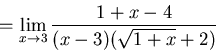


(2) Find the derivatives of the following functions:
(a)
![]()
Looks like a chain rule problem, with the outer function being raising to
the eighth power and the inner
![]() .
So the
derivative is:
.
So the
derivative is:
![]() .
.
(b)
![]()
This is the product of two functions, so the derivative =
the sum of (the first's derivative)*(the second)+ (the first)*
(the second's derivative)=
![]() .
.
(c)
![]()
This one is the quotient of two functions, so it looks like the time and place
to use the quotient rule:
derivative =
![]()
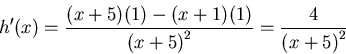
Part 2
(3) Consider
![]() .
.
(a) Where is f(x) not continuous?
f(x) is not continuous where the denominator is 0, namely at the roots of x2-5x-6, or at -1 and 6.
(b) Identify each discontinuity as removable or nonremovable.
-1 is removable while 6 is not removable. This can be verified by checking that the limit of f(x) does not exist as x approaches 6, but it does exist at the point -1. (You should check this, and show this work on the exam).
(c) Where are the vertical asymptotes?
There is a vertical asymptote of x=6, since the right hand limit at 6
is ![]() (also because the left hand limit is
(also because the left hand limit is ![]() -either alone
would make there be an asymptote).
-either alone
would make there be an asymptote).
(4) Calculate the derivative of
![]() using the definition
of the derivative.
using the definition
of the derivative.

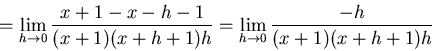
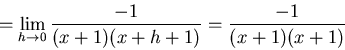
(5) Find the equation of the tangent line to the curve
![]() at the
point
at the
point ![]() .
.
To get the equation of a line we need either: (1) two points or
(2) one point and a slope. We have only one point to work with,
![]() so we need to find the slope. The slope of the tangent line at
that point on the curve is the derivative at that point:
so we need to find the slope. The slope of the tangent line at
that point on the curve is the derivative at that point:
(6) Find the derivative of y with respect to x for the equation:
It would be a great challenge to find an explicit form for the function of y in terms of x, so implicit differentiation is the way to go. First differentiate both sides with respect to x:
The next step is to group the terms with
![]() on the left, the other
terms on the right, so we have:
on the left, the other
terms on the right, so we have:

(7) Find the velocity at impact of a bowling ball dropped from a building
which is 400 feet high, given that the ball has position equation
Velocity can be found by taking the derivative of the position function,
s(t).
v(t)=s'(t)=-32t. But we also need to figure out the time of
impact, or when s(t)=0.
s(t)=-16t2+400=0 when ![]() but the only
one of these which makes physical sense is t=5. Therefore the
velocity of impact is
v(5)= -160feet/second.
but the only
one of these which makes physical sense is t=5. Therefore the
velocity of impact is
v(5)= -160feet/second.