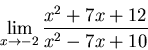
Exam 1 - Limits and Derivatives
Part I
(1) Calculate the following limits (if they exist):
(a)
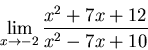
Direct Substitution:
(b)
Direct substitution yields
![]() ,
so further analysis is required.
,
so further analysis is required.
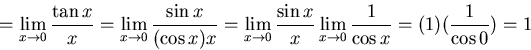
(c)
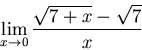
Direct substitution yields
![]() ,
so further analysis is required.
,
so further analysis is required.


(2) Find the derivatives of the following functions:
(a)
![]()
Product Rule:
![]()
(b)
![]()
![]() .
.
(c) h(x) = (x3+3x2+7x+4)(2x5+3x2+2x+1)
Product Rule: (3x2+6x+7)(2x5+3x2+2x+1) + (x3+3x2+7x+4)(10x4+6x+2)
Part 2
(3) Consider
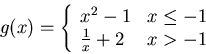
(a) Where is g(x) not continuous?
There is a jump discontinuity at x=-1 because the right and left limits are
different. Also, the function is unbounded at x=0, so this is also a
discontinuity.
(b) Identify each discontinuity as removable or nonremovable.
Both x = 0 and x = -1 are nonremovable.
(c) Where are the vertical asymptotes?
x = 0
(4) Calculate the derivative of f(x)= 3x2+x+1 using the definition of the derivative.
![\begin{displaymath}f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \to 0}
\frac{[3{(x+h)}^2 +(x+h)+1] - (3x^2+x+1)}{h}\end{displaymath}](img14.gif)
(5) Find the equation of the tangent line to the curve
![]() at the
point (0,2).
at the
point (0,2).
The derivative is
![]() ,
so the slope at (0,3) is
,
so the slope at (0,3) is
![]() .
Therefore the equation of the line is:
(y-2)=3(x-0).
.
Therefore the equation of the line is:
(y-2)=3(x-0).
(6) Do one of the following (one is impossible): Give an example of a function which is continuous but not differentiable. Give an example of a function which is differentiable but not continuous.
f(x) = |x| is continuous but not differentiable at x = 0. There are many examples of this direction, but the other direction is impossible.
(7) Find the velocity and acceleration of a ball which is thrown upwards at a
speed of 115 feet per second after 2 seconds. The position equation is
given by:
Velocity is the first derivative and acceleration the second. So v(t) = s'(t) = -32t+96 and a(t)=v'(t) = -32. Thus v(2) = 32ft/s and a(2) = -32ft/s2.
(8) Consider the function f(x) = x3+x2. We want to find the slope of the tangent line to the curve of y=f(x) at the point (1,2).
(a) Estimate the slope by taking slopes of secant lines through the points (1.1, (1.1)2 +(1.1)3), (1.01, (1.01)2+ (1.01)3), and (1+h,(1+h)2 +(1+h)3).
The first two slopes are 5.41 and 5.0401, while the thrid is:
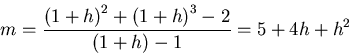
(b) Find the slope by taking the limit of your third answer from (a) as h approaches 0.
![]()
(c) Verify your answer by finding the derivative of the function the easy way, and evaluating at x = 1.
f'(x) = 3x2 + 2x so f'(1) = 3(1) + 2(1) = 5